Hace ya bastantes meses elaboré un programa para procesar las series bursátiles. Naturalmente era un programa a medida que hacía tan solo lo que yo le pedía pero con el que quise mostrar las posibilidades de la programación personalizada para elaborar nuestras propias rutinas de análisis. (Ver: Seguimiento de valores e históricos III ). La arquitectura básica del kit de análisis se basaba en unas macros programadas con imacros que primero nos descargaban los datos en bruto en nuestra computadora. Luego, una vez allí, una serie de scripts programados en Shell Bash, Python y gnuplot procesaban los datos y entregaban como resultado las tablas de datos y los gráficos deseados. El sistema era rígido pues no se trataba más que de un ejemplo para, a partir de él, ir ampliando sus posibilidades. Y eso hice en Stop Loss, volatilidad y ATR donde añadí la capacidad de calcular el susodicho ATR en el programa e incluso de representar gráficamente su variación a lo largo del tiempo.
En la presente entrada dispongo un nuevo añadido. Un análisis de frecuencias de subidas y bajadas bursátiles. Por un lado, vamos a ver cómo se refleja una tendencia en un análisis de frecuencia. Veremos también cómo se perfilan los histogramas para diferentes intervalos temporales. Qué formas tienen y qué es lo que nos pueden decir los números. El proyecto abarcará probablemente varios posts dada su extensión.
Para empezar aquí tenéis la última versión modificada del script en Python. Los añadidos no son muchos como veréis y a los que os guste echarle un vistazo al código os será de utilidad. Mi deseo es ser transparente en todo lo que hago y modifico y por eso lo pongo a vuestra disposición: mm20c55c200ATR_count.py Pero pasemos a detallar sus nuevas prestaciones.
El primer intervalo de tiempo escogido es de 5 años, desde el 2005 hasta el presente. ¿Porqué 5 años? Pues sencillamente porque aproximadamente hace 5 años la bolsa española rondaba los 10.000 puntos, exactamente igual que ahora lo que significa que tras 5 años de subidas y bajadas no ha habido grandes cambios en el valor del índice o lo que es lo mismo para un plazo de 5 años el Ibex presenta tendencia lateral. Fijémonos en el gráfico:


Como vemos empieza y termina en el mismo punto. Estamos como hace 5 años, ni más ni menos. En tendencia lateral en el largo plazo.
Dado que el plazo es muy grande, unas 1200 sesiones, podremos estar seguros que los valores obtenidos obedecen a la ley de los grandes números. Esto es, nos tiene que salir una función Gausiana muy definida. ¿Será así?
Para ser exactos, nuestro programa empieza el conteo desde el día 14 de octubre de 2005 día en que la bolsa cerró en los 10629,3 puntos y termina el 22 de julio de 2010 cuando cerró a 10302,9 puntos. Es decir que en el intervalo de conteo la bolsa ha descendido apenas poco más 300 puntos. No es gran cosa si tenemos en cuenta que hay unos 5 años de diferencia entre ambas fechas.
El programa calcula la variación en la cotización a lo largo del intradía, precio de cierre - precio de apertura, y la variación diaria real de la cotización, precio de cierre - precio de cierre del día anterior. Esta última sí tiene en cuenta los saltos o huecos de apertura. El programa efectúa estas sencillas restas para cada sesión. Luego con todos esos valores calcula tres porcentajes para cada valor o índice. El porcentaje de días en que la cotización sube, el porcentaje en que los precios bajan y el porcentaje en el que mantienen su precio, variación nula, es decir, en el que el valor final coincide con el inicial.
El programa imprime por pantalla los resultados pero también genera un fichero, "results.dat", donde quedan registradas algunas de las variables que considero más importantes para así poder volver a ellos cuando nos plazca. Como digimos, con 1200 sesiones de registros es previsible que los resultados obedezcan bien la ley de los grandes números. Los que me habéis seguido sabréis que confeccioné ya hace bastantes meses una lista de valores a seguir en Seguimiento de valores e históricos II justificando mis razones. Puede que en mi lista consideréis que sobren algunos valores y que falten otros. Es posible pero en cualquier caso es una lista con diversas empresas del Ibex y con algunas europeas y americanas bien conocidas. Además contiene unos cuantos índices importantes desde el propio Ibex al DowJones Industrial. Tengo pendiente de hacer unas listas de valores mucho más completas y extensas que serían recogidas por nuevas macros. Por falta de tiempo eso es algo a lo que aun no me he dedicado y para lo que nos ocupa esta lista es suficientemente variada e interesante.
En la siguiente tabla de Excel ( conteos.xls ) os paso los resultados iniciales del programa. La primera columna muestra las acciones en minúsculas y los índices en mayúsculas. La segunda es el porcentaje de ATR14 respecto al precio de la acción de los últimos días. A mayor sea el valor mayor la volatilidad. Para más información sobre éste indicador revisar la entrada que hice sobre la volatilidad. Las siguientes columnas se dividen en dos bloques de 3. El primer bloque muestra los porcentajes de subidas y bajadas en el intradía y el segundo bloque tiene en cuenta los huecos.
Si observamos los resultados vemos que en la gran mayoría de casos los porcentajes de subidas y de bajadas rondan el 50% y que los porcentajes de variación nula rondan el 1 al 2 % en el caso de las acciones y el 0% en el de los índices. Todo parece responder a la lógica del azar. Resulta lógico que la cantidad de días que los valores no varían sea bajo ya que es un hecho improbable. Dado que los índices son, más líquidos por decirlo así, casi nunca terminan con el mismo precio que empezaronla sesión. En cambio valores grandes de ese porcentaje pueden indicar una falta de liquidez del valor como es el caso de CAF con un 12,6% o Aguas de Barcelona con un 8,5%. En estos valores hay menos variación en el intradía por lo que las probabilidades de que su cierre coincida con el cierre del día anterior son mayores.
Ahora centrémonos en el Ibex. Aquí tenéis la tabla de cotizaciones e indicadores del Ibex calculados por el programa en formato de texto ( ibex_diaria_1.dat ). Recordemos que hemos dicho que en dicho intervalo la valoración del índice apenas sí ha variado, de hecho ha descendido en unos 300 puntos. Si miramos los porcentajes en cambio encontramos que el 53,5% de los días durante dicho intervalo la bolsa ha subido. Eso significa lo que ya venimos diciendo en entradas anteriores y que queda definitivamente corroborado por los números y es que la bolsa baja menos días pero baja más fuerte. Es algo que ya se intuye viendo el gráfico pero que quería demostrarlo numéricamente ya que a veces las cosas no son como nos dice la intuición.
Un primer dato interesante es que durante dicho periodo, el 83% de veces el sentido de la variación verdadera, incluyendo el gap, coincide con la el sentido de la variación intradía. Esto es relevante por cuanto demuestra que el gap no tiene mucha influencia en el índice. Esto no tiene porque ser así en las acciones donde probablemente tengan más peso.
Pero para analizar más a fondo la información nos puede ser muy útil realizar histogramas. Los histogramas usualmente son unos gráficos de barras en los que cada barra representa un intervalo, bin, y su altura la frecuencia de ocurrencia de dicho intervalo. Como ya hemos dicho antes, la distribución de frecuencias esperamos que sea aproximadamente gausiana dado que estamos computando sobre 1200 sesiones, un valor suficientemente grande como para que el peso de la estadística aleatoria se imponga. Veamos:
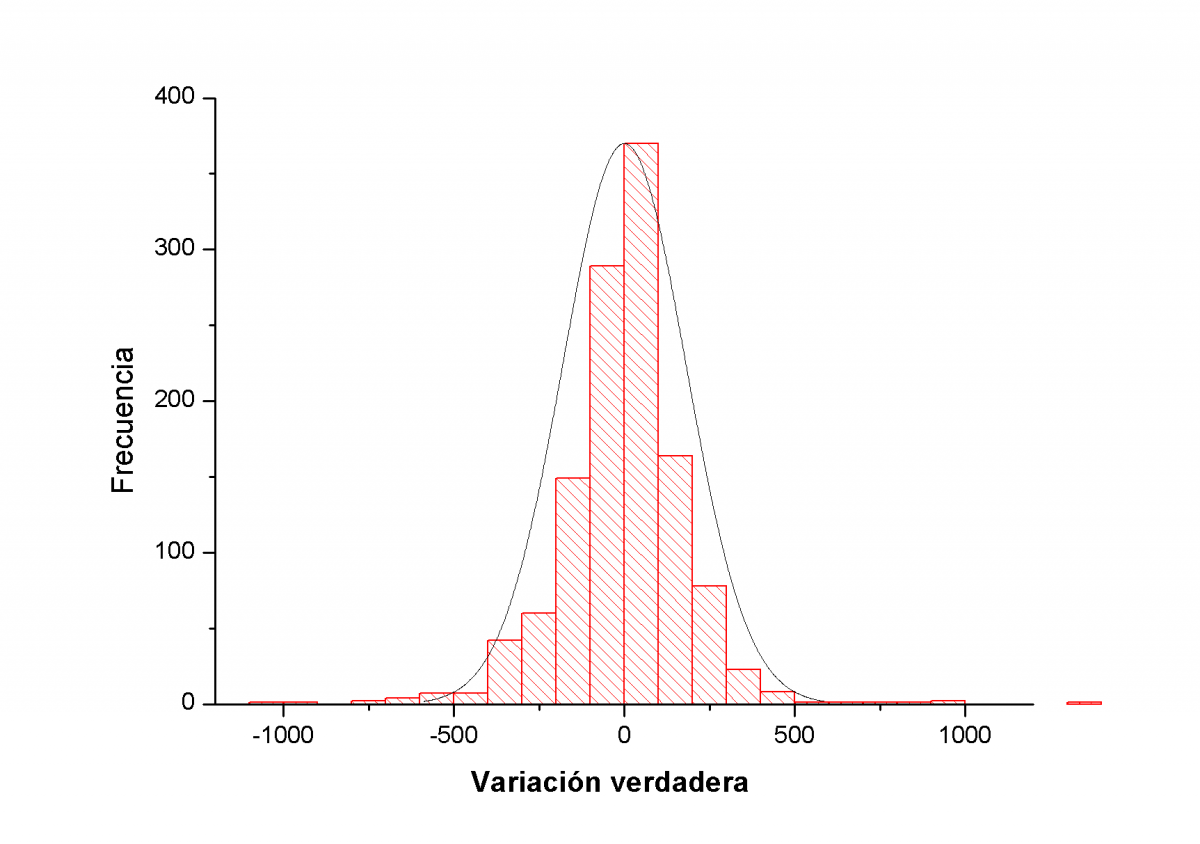
Lo que aquí vemos es que si bien el histograma refleja una cuasi gausiana centrada en el 0 esto no es así exactamente. Fijémonos en las diferencias. De entrada el máximo está desplazado hacia la zona positiva lo que confirma el dato de que en dicho intervalo ha habido más subidas que bajadas. Por otra parte las colas no son iguales. Si nos fijamos bien la cola de las bajadas fuertes es más grande que la de las subidas fuertes lo que nos confirma que las bajadas son minoría pero que suman más que las subidas. Nuevamente demostramos al anterior enunciado en negrita.
Análisis con el mercado en tendencia
Todos estos resultados, como ya he mos dicho, son en un mercado de tendencia lateral a 5 años vista. Un plazo enorme. Pero ¿que ocurre con tendencias de más corto plazo? También me lo he preguntado y también lo he calculado. Veamos el histograma del Ibex durante la fuerte tendencia alcista desde mínimos de marzo. El periodo de estudio es del 9 de marzo de 2009 al 6 de enero de 2010.
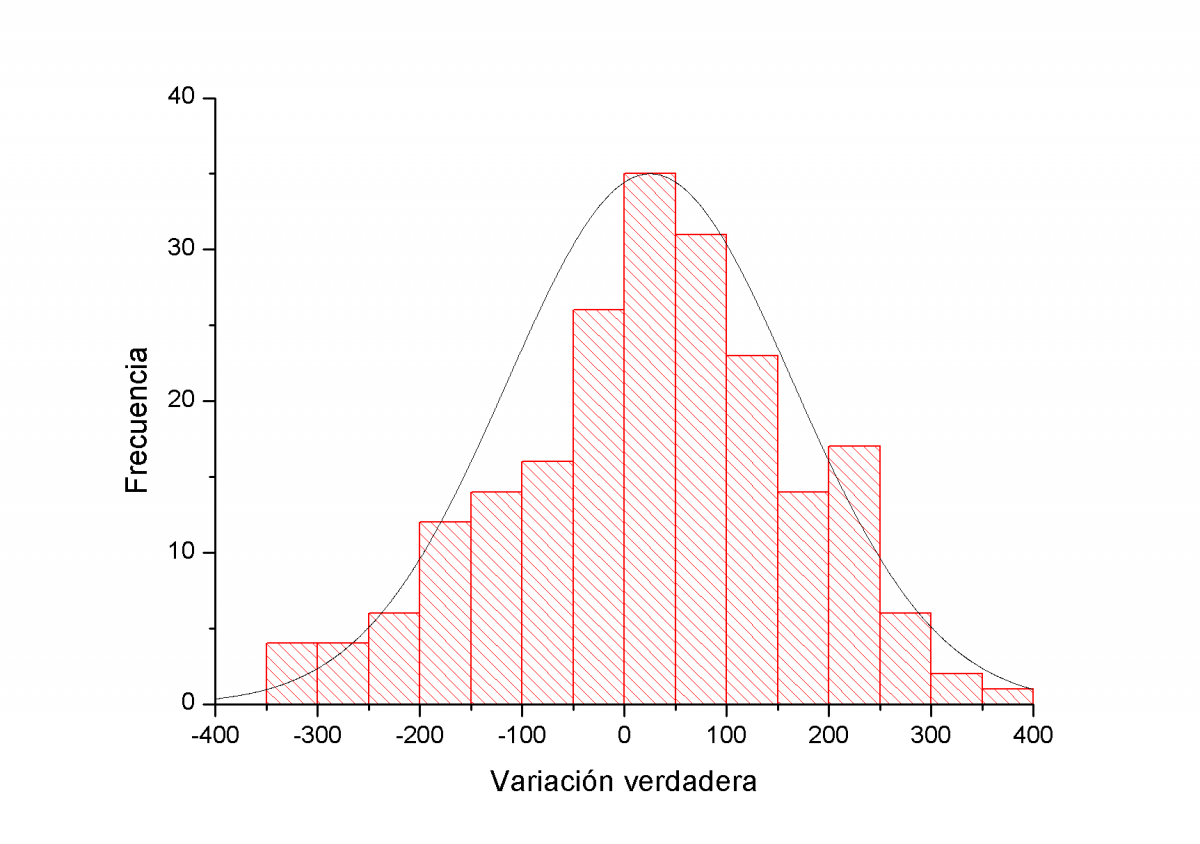
Este histograma presenta un perfil mucho menos definido. Como vemos se ajusta mucho peor a una gausiana algo lógico ya que ahora tan solo contamos con algo más de 200 sesiones mientras que el anterior histograma contaba sobre 1200. Otra diferencia destacable es que ahora la gausiana está claramente centrada en el lado positivo de la variación verdadera de un dia a otro. Alrededor de los 25 puntos. El porcentaje de días alcistas es ahora del 61% y el de días bajistas del 39%. En este caso ambas colas están mucho más igualadas que en el caso anterior.
Ahora veamos qué ocurre con el histograma de la tendencia bajista reciente. Esta tendencia, hasta la fecha, abarca muy pocas sesiones. La física de los desplomes nos dice que estos son siempre más breves pero más catastróficos. Es decir que existe una asimetría entre tendencias alcistas y bajistas. Algún día de estos entraré en detalle en estos aspectos y su posible análisis econofísico.
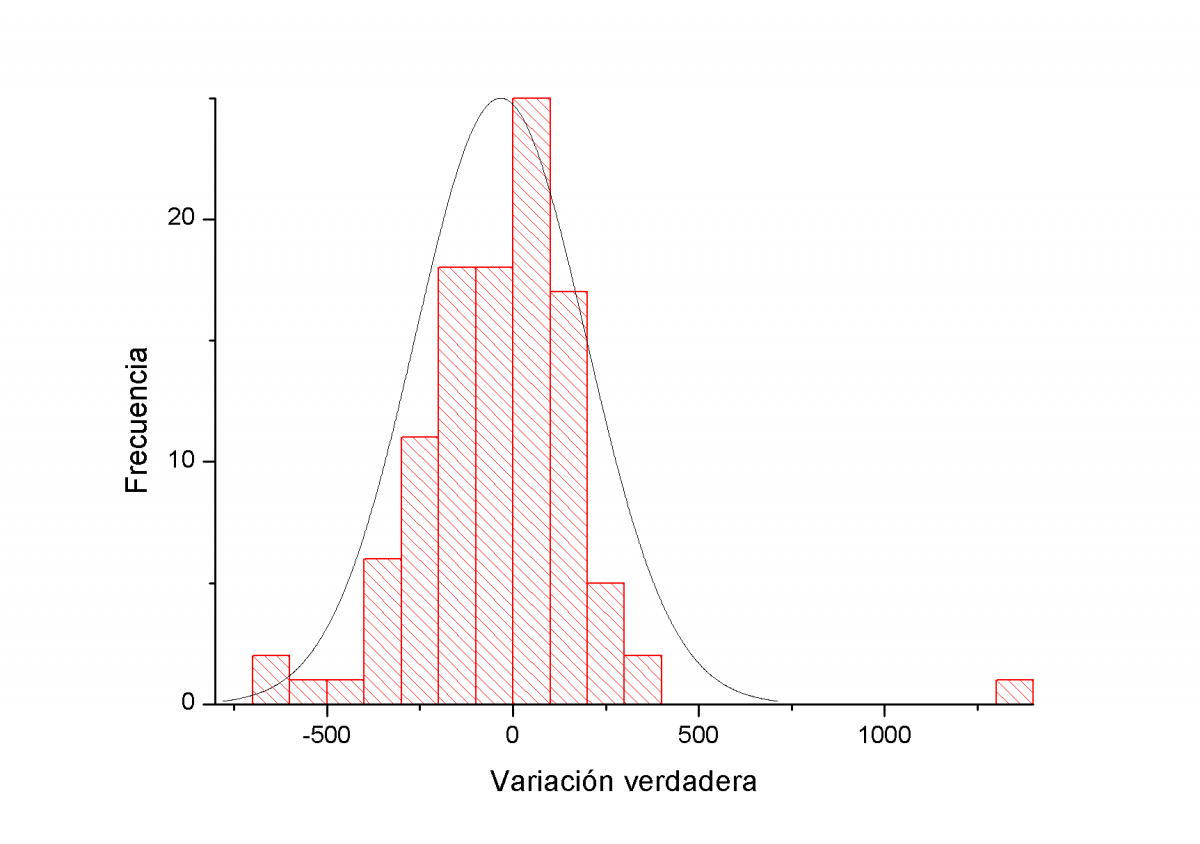
Dado que las sesiones bajistas suelen ser más acusadas que las alcistas basta una leve descompensación en favor de las sesiones bajistas para que ello se refleje en una fuerte tendencia a la baja. De hecho, en dicho período hay un 53% de sesiones bajistas y un 47% de alcistas nada que ver con los porcentajes anteriores, como vemos. La cola bajista es mucho mas gruesa como se ve, destaca también una jornada alcista enorme, un suceso fuera de lo corriente. Hay que tener en cuenta que a veces, estas cosas ocurren, probablemente en este caso fue un cierre de cortos, un pánico comprador, son raros, mucho más que los pánicos vendedores pero pueden darse en periodos de fuertes bajadas en forma de rebotes repentinos. Estos raros eventos de una sola sesión a veces pueden bastar para invertir una tendencia, otras veces no como es el caso que vemos.
---------------------------------------------------------
Conclusiones:
Este es un ejercicio numérico que deseaba hacer y que espero ir ampliando en otras entradas a medida que vaya perfeccionando y ampliando mis análisis. Las posibilidades a medida que se añade complejidad son ilimitadas. Pueden analizarse histogramas de muchas más variables, los gaps por ejemplo, sobre acciones, sobre otros índices, luego ponerlas en relación para buscar correlaciones o simplemente amasar todos los datos en un bloque compacto para clusterizarlo posteriormente mediante algoritmos más potentes. Por ahora he empezado por validar mediante mis propios medios una afirmación que la intuición parecía validar. Pero como siempre digo los números están ahí para que los utilicemos, los números pueden hablar. ¿Lo que un analista de datos espera encontrar de todo esto? Quien sabe. Lo cierto es que los mejores hallazgos son los que nadie esperaría encontrar. Pero no me quedaré aquí. También quiero explorar la física que hay detrás de los desplomes bursátiles y por supuesto estos análisis no impediran que siga con el ahorro y en los aspectos más terrenales de la estrategia que seguiré plasmando aquí siempre que mi tiempo me lo permita, seguiremos hablando de todo ello y de mucho más. Y siempre recordando que las oscilaciones de la bolsa son, ante todo un fenómeno estocástico y no lineal así que el santo grial no existe como no lo existe sobre cualquier otro sistema de esa índole como la predicción de terremotos.
Un saludo ahorradores y hasta la próxima.
